Algoritmo

Após o usuário gerar a curva, o sistema inicialmente efetua uma reamostragem uniforme da mesma, esta operação não é essencial, mas seu uso permite a geração de malhas mais uniformes.

Figura: Curva original e reamostrada.

A curva reamostrada passa então por um processo de suavização, para evitar possíveis traços "tremidos", esta operação também não é essencial ao algoritmo, mas os resultados em geral são mais satisfatórios quando ela é usada.

Figura: Curva reamostrada e suavizada.

Em seguida calcula-se uma triangulação de Delaunay com restrições CDT (Constrained Delaunay Triangulation). Para isto, foi utilizado o código TRIANGLE (http://www.cs.cmu.edu/~quake/triangle.html).

Figura: Triangulação de Delaunay com restrições.

Podemos dividir os triângulos da CDT em dois grupos: triângulos internos e externos, onde os internos são aqueles contidos na região delimitada pela curva, enquanto os outros são os externos. Serão utilizados apenas os triângulos internos, que por sua vez podem ser classificados em três tipos:

• Terminal: triângulos que possuem duas arestas pertencentes à curva.
• Sleeve: triângulos que possuem apenas uma aresta pertencente à curva.
• Joint: triângulos que não possuem arestas pertencentes à curva.

Figura: Tipos de triângulos da CDT: em vermelho triângulos Joint; em verde triângulos Sleeve; em azul triângulos do tipo Terminal.

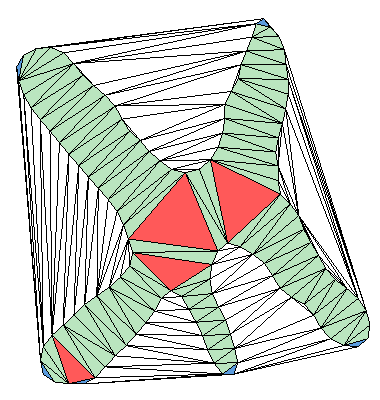Para melhores resultados, podemos modificar alguns triângulos. Quando um triângulo Terminal está muito próximo a um Joint podemos rearrumar os triângulos envolvidos, tornando-os todos do tipo Sleeve, conforme ilustra a figura:

Figura: Processo de reordenação de triângulos.

Figura: Triângulos da CDT após reordenação.

Tendo os triângulos classificados, constroi-se então uma malha triangular da seguinte maneira:

Dada uma aresta da CDT que não seja aresta da curva de entrada, defina "circunferência transversal" a circunferência que passa pelos vértices desta aresta e que é perpendicular ao plano da curva.

Em cada triângulo do tipo terminal calculam-se pontos sobre a circunferência transversal que contém os pontos da aresta interna. Adicionam-se então à malha triângulos formados ao se ligarem os pontos desta circunferência ao terceiro vértice do triângulo Terminal. Conforme ilustra a figura abaixo:

Figura: Triangulação a partir de triângulo Terminal.

Em cada triângulo do tipo Joint, calculam-se triângulos sobre a esfera cujo centro é o circuncentro do triângulo Joint e cujo raio é o raio do circuncírculo deste triângulo. Conforme ilustra a figura:

Figura: Triangulação a partir de triângulo Joint.

Em cada triângulo do tipo Sleeve, verifica-se primeiramente se é possível fazer uma união deste com um de seus vizinhos, o que acontece quando as arestas da curva destes triângulos estão em lados opostos, no caso afirmativo adicionam-se à malha triângulos conectando as circunferências transversais que estão em lados opostos, conforme ilustra a figura:

Figura: Triangulação a partir de dois triângulos Sleeve.

Caso não seja possível unir dois triângulos Sleeve vizinhos, adicionam-se à malha triângulos conectando as circunferências transversais do Sleeve determinado.

Figura: Triangulação a partir de um triângulo Sleeve.

Os vértices dos triângulos adicionados à malha devem ser calculados de forma que ao final do processo tenhamos uma malha fechada formando uma triangulação consistente.

Figura: Malha triangular gerada.

Figura: Renderização flat shading da malha triangular.